Method of steepest descent
In mathematics, the method of steepest descent or stationary-phase method or saddle-point method is an extension of Laplace's method for approximating an integral, where one deforms a contour integral in the complex plane to pass near a stationary point (saddle point), in roughly the direction of steepest descent or stationary phase. The saddle-point approximation is used with integrals in the complex plane, whereas Laplace’s method is used with real integrals.
The integral to be estimated is often of the form
- ∫Cf(z)eλg(z)dz,{displaystyle int _{C}f(z)e^{lambda g(z)},dz,}
where C is a contour, and λ is large. One version of the method of steepest descent deforms the contour of integration C into a new path integration C′ so that the following conditions hold:
C′ passes through one or more zeros of the derivative g′(z),- the imaginary part of g(z) is constant on C′.
The method of steepest descent was first published by Debye (1909), who used it to estimate Bessel functions and pointed out that it occurred in the unpublished note Riemann (1863) about hypergeometric functions. The contour of steepest descent has a minimax property, see Fedoryuk (2001). Siegel (1932) described some other unpublished notes of Riemann, where he used this method to derive the Riemann–Siegel formula.
Contents
1 A simple estimate[1]
2 The case of a single non-degenerate saddle point
2.1 Basic notions and notation
2.2 Complex Morse lemma
2.3 The asymptotic expansion in the case of a single non-degenerate saddle point
3 The case of multiple non-degenerate saddle points
4 The other cases
5 Extensions and generalizations
6 See also
7 Notes
8 References
A simple estimate[1]
Let f, S : Cn → C and C ⊂ Cn. If
- M=supx∈Cℜ(S(x))<∞,{displaystyle M=sup _{xin C}Re (S(x))<infty ,}
where ℜ(⋅){displaystyle Re (cdot )}
- ∫C|f(x)eλ0S(x)|dx<∞,{displaystyle int _{C}left|f(x)e^{lambda _{0}S(x)}right|dx<infty ,}
then the following estimate holds:
- |∫Cf(x)eλS(x)dx|⩽const⋅eλM,∀λ∈R,λ⩾λ0.{displaystyle left|int _{C}f(x)e^{lambda S(x)}dxright|leqslant {text{const}}cdot e^{lambda M},qquad forall lambda in mathbb {R} ,quad lambda geqslant lambda _{0}.}
- |∫Cf(x)eλS(x)dx|⩽∫C|f(x)||eλS(x)|dx≡∫C|f(x)|eλM|eλ0(S(x)−M)e(λ−λ0)(S(x)−M)|dx⩽∫C|f(x)|eλM|eλ0(S(x)−M)|dx|e(λ−λ0)(S(x)−M)|⩽1=e−λ0M∫C|f(x)eλ0S(x)|dx⏟const⋅eλM.{displaystyle {begin{aligned}left|int _{C}f(x)e^{lambda S(x)}dxright|&leqslant int _{C}|f(x)|left|e^{lambda S(x)}right|dx\&equiv int _{C}|f(x)|e^{lambda M}left|e^{lambda _{0}(S(x)-M)}e^{(lambda -lambda _{0})(S(x)-M)}right|dx\&leqslant int _{C}|f(x)|e^{lambda M}left|e^{lambda _{0}(S(x)-M)}right|dx&&left|e^{(lambda -lambda _{0})(S(x)-M)}right|leqslant 1\&=underbrace {e^{-lambda _{0}M}int _{C}left|f(x)e^{lambda _{0}S(x)}right|dx} _{text{const}}cdot e^{lambda M}.end{aligned}}}
The case of a single non-degenerate saddle point
Basic notions and notation
Let x be a complex n-dimensional vector, and
- Sxx″(x)≡(∂2S(x)∂xi∂xj),1⩽i,j⩽n,{displaystyle S''_{xx}(x)equiv left({frac {partial ^{2}S(x)}{partial x_{i}partial x_{j}}}right),qquad 1leqslant i,,jleqslant n,}
denote the Hessian matrix for a function S(x). If
- φ(x)=(φ1(x),φ2(x),…,φk(x)){displaystyle {boldsymbol {varphi }}(x)=(varphi _{1}(x),varphi _{2}(x),ldots ,varphi _{k}(x))}
is a vector function, then its Jacobian matrix is defined as
- φx′(x)≡(∂φi(x)∂xj),1⩽i⩽k,1⩽j⩽n.{displaystyle {boldsymbol {varphi }}_{x}'(x)equiv left({frac {partial varphi _{i}(x)}{partial x_{j}}}right),qquad 1leqslant ileqslant k,quad 1leqslant jleqslant n.}
A non-degenerate saddle point, z0 ∈ Cn, of a holomorphic function S(z) is a critical point of the function (i.e., ∇S(z0) = 0) where the function's Hessian matrix has a non-vanishing determinant (i.e., detSzz″(z0)≠0{displaystyle det S''_{zz}(z^{0})neq 0}
The following is the main tool for constructing the asymptotics of integrals in the case of a non-degenerate saddle point:
Complex Morse lemma
The Morse lemma for real-valued functions generalizes as follows[2] for holomorphic functions: near a non-degenerate saddle point z0 of a holomorphic function S(z), there exist coordinates in terms of which S(z) − S(z0) is exactly quadratic. To make this precise, let S be a holomorphic function with domain W ⊂ Cn, and let z0 in W be a non-degenerate saddle point of S, that is, ∇S(z0) = 0 and detSzz″(z0)≠0{displaystyle det S''_{zz}(z^{0})neq 0}
- ∀w∈V:S(φ(w))=S(z0)+12∑j=1nμjwj2,detφw′(0)=1,{displaystyle forall win V:qquad S({boldsymbol {varphi }}(w))=S(z^{0})+{frac {1}{2}}sum _{j=1}^{n}mu _{j}w_{j}^{2},quad det {boldsymbol {varphi }}_{w}'(0)=1,}
Here, the μj are the eigenvalues of the matrix Szz″(z0){displaystyle S_{zz}''(z^{0})}
An illustration of Complex Morse lemma
The following proof is a straightforward generalization of the proof of the real Morse Lemma, which can be found in.[3] We begin by demonstrating
Auxiliary statement. Let f : Cn → C be holomorphic in a neighborhood of the origin and f (0) = 0. Then in some neighborhood, there exist functions gi : Cn → C such that
- f(z)=∑i=1nzigi(z),{displaystyle f(z)=sum _{i=1}^{n}z_{i}g_{i}(z),}
- f(z)=∑i=1nzigi(z),{displaystyle f(z)=sum _{i=1}^{n}z_{i}g_{i}(z),}
- where each gi is holomorphic and
- gi(0)=∂f(z)∂zi|z=0.{displaystyle g_{i}(0)=left.{tfrac {partial f(z)}{partial z_{i}}}right|_{z=0}.}
- gi(0)=∂f(z)∂zi|z=0.{displaystyle g_{i}(0)=left.{tfrac {partial f(z)}{partial z_{i}}}right|_{z=0}.}
From the identity
- f(z)=∫01ddtf(tz1,⋯,tzn)dt=∑i=1nzi∫01∂f(z)∂zi|z=(tz1,…,tzn)dt,{displaystyle f(z)=int _{0}^{1}{frac {d}{dt}}fleft(tz_{1},cdots ,tz_{n}right)dt=sum _{i=1}^{n}z_{i}int _{0}^{1}left.{frac {partial f(z)}{partial z_{i}}}right|_{z=(tz_{1},ldots ,tz_{n})}dt,}
we conclude that
- gi(z)=∫01∂f(z)∂zi|z=(tz1,…,tzn)dt{displaystyle g_{i}(z)=int _{0}^{1}left.{frac {partial f(z)}{partial z_{i}}}right|_{z=(tz_{1},ldots ,tz_{n})}dt}
and
- gi(0)=∂f(z)∂zi|z=0.{displaystyle g_{i}(0)=left.{frac {partial f(z)}{partial z_{i}}}right|_{z=0}.}
Without loss of generality, we translate the origin to z0, such that z0 = 0 and S(0) = 0. Using the Auxiliary Statement, we have
- S(z)=∑i=1nzigi(z).{displaystyle S(z)=sum _{i=1}^{n}z_{i}g_{i}(z).}
Since the origin is a saddle point,
- ∂S(z)∂zi|z=0=gi(0)=0,{displaystyle left.{frac {partial S(z)}{partial z_{i}}}right|_{z=0}=g_{i}(0)=0,}
we can also apply the Auxiliary Statement to the functions gi(z) and obtain
S(z)=∑i,j=1nzizjhij(z).{displaystyle S(z)=sum _{i,j=1}^{n}z_{i}z_{j}h_{ij}(z).}(1)
Recall that an arbitrary matrix A can be represented as a sum of symmetric A(s) and anti-symmetric A(a) matrices,
- Aij=Aij(s)+Aij(a),Aij(s)=12(Aij+Aji),Aij(a)=12(Aij−Aji).{displaystyle A_{ij}=A_{ij}^{(s)}+A_{ij}^{(a)},qquad A_{ij}^{(s)}={tfrac {1}{2}}left(A_{ij}+A_{ji}right),qquad A_{ij}^{(a)}={tfrac {1}{2}}left(A_{ij}-A_{ji}right).}
The contraction of any symmetric matrix B with an arbitrary matrix A is
- ∑i,jBijAij=∑i,jBijAij(s),{displaystyle sum _{i,j}B_{ij}A_{ij}=sum _{i,j}B_{ij}A_{ij}^{(s)},}
i.e., the anti-symmetric component of A does not contribute because
- ∑i,jBijCij=∑i,jBjiCji=−∑i,jBijCij=0.{displaystyle sum _{i,j}B_{ij}C_{ij}=sum _{i,j}B_{ji}C_{ji}=-sum _{i,j}B_{ij}C_{ij}=0.}
Thus, hij(z) in equation (1) can be assumed to be symmetric with respect to the interchange of the indices i and j. Note that
- ∂2S(z)∂zi∂zj|z=0=2hij(0);{displaystyle left.{frac {partial ^{2}S(z)}{partial z_{i}partial z_{j}}}right|_{z=0}=2h_{ij}(0);}
hence, det(hij(0)) ≠ 0 because the origin is a non-degenerate saddle point.
Let us show by induction that there are local coordinates u = (u1, ... un), z = ψ(u), 0 = ψ(0), such that
S(ψ(u))=∑i=1nui2.{displaystyle S({boldsymbol {psi }}(u))=sum _{i=1}^{n}u_{i}^{2}.}(3)
First, assume that there exist local coordinates y = (y1, ... yn), z = φ(y), 0 = φ(0), such that
S(ϕ(y))=y12+⋯+yr−12+∑i,j=rnyiyjHij(y),{displaystyle S({boldsymbol {phi }}(y))=y_{1}^{2}+cdots +y_{r-1}^{2}+sum _{i,j=r}^{n}y_{i}y_{j}H_{ij}(y),}(4)
where Hij is symmetric due to equation (2). By a linear change of the variables (yr, ... yn), we can assure that Hrr(0) ≠ 0. From the chain rule, we have
- ∂2S(ϕ(y))∂yi∂yj=∑l,k=1n∂2S(z)∂zk∂zl|z=ϕ(y)∂ϕk∂yi∂ϕl∂yj+∑k=1n∂S(z)∂zk|z=ϕ(y)∂2ϕk∂yi∂yj{displaystyle {frac {partial ^{2}S({boldsymbol {phi }}(y))}{partial y_{i}partial y_{j}}}=sum _{l,k=1}^{n}left.{frac {partial ^{2}S(z)}{partial z_{k}partial z_{l}}}right|_{z={boldsymbol {phi }}(y)}{frac {partial phi _{k}}{partial y_{i}}}{frac {partial phi _{l}}{partial y_{j}}}+sum _{k=1}^{n}left.{frac {partial S(z)}{partial z_{k}}}right|_{z={boldsymbol {phi }}(y)}{frac {partial ^{2}phi _{k}}{partial y_{i}partial y_{j}}}}
Therefore:
- Syy″(ϕ(0))=ϕy′(0)TSzz″(0)ϕy′(0),detϕy′(0)≠0;{displaystyle S''_{yy}({boldsymbol {phi }}(0))={boldsymbol {phi }}'_{y}(0)^{T}S''_{zz}(0){boldsymbol {phi }}'_{y}(0),qquad det {boldsymbol {phi }}'_{y}(0)neq 0;}
whence,
- 0≠detSyy″(ϕ(0))=2r−1det(2Hij(0)).{displaystyle 0neq det S''_{yy}({boldsymbol {phi }}(0))=2^{r-1}det left(2H_{ij}(0)right).}
The matrix (Hij(0)) can be recast in the Jordan normal form: (Hij(0)) = LJL−1, were L gives the desired non-singular linear transformation and the diagonal of J contains non-zero eigenvalues of (Hij(0)). If Hij(0) ≠ 0 then, due to continuity of Hij(y), it must be also non-vanishing in some neighborhood of the origin. Having introduced H~ij(y)=Hij(y)/Hrr(y){displaystyle {tilde {H}}_{ij}(y)=H_{ij}(y)/H_{rr}(y)}
- S(φ(y))=y12+⋯+yr−12+Hrr(y)∑i,j=rnyiyjH~ij(y)=y12+⋯+yr−12+Hrr(y)[yr2+2yr∑j=r+1nyjH~rj(y)+∑i,j=r+1nyiyjH~ij(y)]=y12+⋯+yr−12+Hrr(y)[(yr+∑j=r+1nyjH~rj(y))2−(∑j=r+1nyjH~rj(y))2]+Hrr(y)∑i,j=r+1nyiyjH~ij(y){displaystyle {begin{aligned}S({boldsymbol {varphi }}(y))=&y_{1}^{2}+cdots +y_{r-1}^{2}+H_{rr}(y)sum _{i,j=r}^{n}y_{i}y_{j}{tilde {H}}_{ij}(y)\=&y_{1}^{2}+cdots +y_{r-1}^{2}+H_{rr}(y)left[y_{r}^{2}+2y_{r}sum _{j=r+1}^{n}y_{j}{tilde {H}}_{rj}(y)+sum _{i,j=r+1}^{n}y_{i}y_{j}{tilde {H}}_{ij}(y)right]\=&y_{1}^{2}+cdots +y_{r-1}^{2}+H_{rr}(y)left[left(y_{r}+sum _{j=r+1}^{n}y_{j}{tilde {H}}_{rj}(y)right)^{2}-left(sum _{j=r+1}^{n}y_{j}{tilde {H}}_{rj}(y)right)^{2}right]+H_{rr}(y)sum _{i,j=r+1}^{n}y_{i}y_{j}{tilde {H}}_{ij}(y)end{aligned}}}
![begin{align}<br />
S(boldsymbol{varphi}(y)) =& y_1^2 + cdots + y_{r-1}^2 + H_{rr}(y) sum_{i,j = r}^n y_i y_j tilde{H}_{ij} (y) \<br />
=& y_1^2 + cdots + y_{r-1}^2 + H_{rr}(y)left[ y_r^2 + 2y_r sum_{j=r+1}^n y_j tilde{H}_{rj} (y) + sum_{i,j = r+1}^n y_i y_j tilde{H}_{ij} (y) right] \<br />
=& y_1^2 + cdots + y_{r-1}^2 + H_{rr}(y)left[ left( y_r + sum_{j=r+1}^n y_j tilde{H}_{rj} (y)right)^2 - left( sum_{j=r+1}^n y_j tilde{H}_{rj} (y)right)^2 right] + H_{rr}(y) sum_{i,j = r+1}^n y_i y_j tilde{H}_{ij}(y) <br />
end{align}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c6897bd4bcd2f3e6b2ed9ee4a071351b07ec6522)
Motivated by the last expression, we introduce new coordinates z = η(x), 0 = η(0),
- xr=Hrr(y)(yr+∑j=r+1nyjH~rj(y)),xj=yj,∀j≠r.{displaystyle x_{r}={sqrt {H_{rr}(y)}}left(y_{r}+sum _{j=r+1}^{n}y_{j}{tilde {H}}_{rj}(y)right),qquad x_{j}=y_{j},quad forall jneq r.}
The change of the variables y ↔ x is locally invertible since the corresponding Jacobian is non-zero,
- ∂xr∂yk|y=0=Hrr(0)[δr,k+∑j=r+1nδj,kH~jr(0)].{displaystyle left.{frac {partial x_{r}}{partial y_{k}}}right|_{y=0}={sqrt {H_{rr}(0)}}left[delta _{r,,k}+sum _{j=r+1}^{n}delta _{j,,k}{tilde {H}}_{jr}(0)right].}
![left. frac{partial x_r}{partial y_k} right|_{y=0} = sqrt{H_{rr}(0)} left[ delta_{r,, k} + sum_{j=r+1}^n delta_{j, , k} tilde{H}_{jr}(0) right].](https://wikimedia.org/api/rest_v1/media/math/render/svg/31789a60384c5526af564f02843e6aff3065930c)
Therefore,
S(η(x))=x12+⋯+xr2+∑i,j=r+1nxixjWij(x).{displaystyle S({boldsymbol {eta }}(x))={x}_{1}^{2}+cdots +{x}_{r}^{2}+sum _{i,j=r+1}^{n}{x}_{i}{x}_{j}W_{ij}(x).}(5)
Comparing equations (4) and (5), we conclude that equation (3) is verified. Denoting the eigenvalues of Szz″(0){displaystyle S''_{zz}(0)}
S(φ(w))=12∑j=1nμjwj2.{displaystyle S({boldsymbol {varphi }}(w))={frac {1}{2}}sum _{j=1}^{n}mu _{j}w_{j}^{2}.}(6)
Therefore,
Sww″(φ(0))=φw′(0)TSzz″(0)φw′(0),{displaystyle S''_{ww}({boldsymbol {varphi }}(0))={boldsymbol {varphi }}'_{w}(0)^{T}S''_{zz}(0){boldsymbol {varphi }}'_{w}(0),}(7)
From equation (6), it follows that detSww″(φ(0))=μ1⋯μn{displaystyle det S''_{ww}({boldsymbol {varphi }}(0))=mu _{1}cdots mu _{n}}
- detSww″(φ(0))=[detφw′(0)]2detSzz″(0)⟹detφw′(0)=±1.{displaystyle det S''_{ww}({boldsymbol {varphi }}(0))=left[det {boldsymbol {varphi }}'_{w}(0)right]^{2}det S''_{zz}(0)Longrightarrow det {boldsymbol {varphi }}'_{w}(0)=pm 1.}
![det S''_{ww} (boldsymbol{varphi}(0)) = left[det boldsymbol{varphi}'_w(0) right]^2 det S''_{zz}(0) Longrightarrow det boldsymbol{varphi}'_w(0) = pm 1.](https://wikimedia.org/api/rest_v1/media/math/render/svg/64f03f4136b8cea03e8a7418fd989c79469d1250)
If detφw′(0)=−1{displaystyle det {boldsymbol {varphi }}'_{w}(0)=-1}
The asymptotic expansion in the case of a single non-degenerate saddle point
Assume
f (z) and S(z) are holomorphic functions in an open, bounded, and simply connected set Ωx ⊂ Cn such that the Ix = Ωx ∩ Rn is connected;
ℜ(S(z)){displaystyle Re (S(z))}has a single maximum: maxz∈Ixℜ(S(z))=ℜ(S(x0)){displaystyle max _{zin I_{x}}Re (S(z))=Re (S(x^{0}))}
for exactly one point x0 ∈ Ix;
x0 is a non-degenerate saddle point (i.e., ∇S(x0) = 0 and detSxx″(x0)≠0{displaystyle det S''_{xx}(x^{0})neq 0}).
Then, the following asymptotic holds
I(λ)≡∫Ixf(x)eλS(x)dx=(2πλ)n2eλS(x0)(f(x0)+O(λ−1))∏j=1n(−μj)−12,λ→∞,{displaystyle I(lambda )equiv int _{I_{x}}f(x)e^{lambda S(x)}dx=left({frac {2pi }{lambda }}right)^{frac {n}{2}}e^{lambda S(x^{0})}left(f(x^{0})+Oleft(lambda ^{-1}right)right)prod _{j=1}^{n}(-mu _{j})^{-{frac {1}{2}}},qquad lambda to infty ,}(8)
where μj are eigenvalues of the Hessian Sxx″(x0){displaystyle S''_{xx}(x^{0})}
- |arg−μj|<π4.{displaystyle left|arg {sqrt {-mu _{j}}}right|<{tfrac {pi }{4}}.}
This statement is a special case of more general results presented in Fedoryuk (1987).[4]
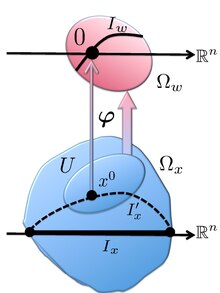
An illustration to the derivation of equation (8)
First, we deform the contour Ix into a new contour Ix′⊂Ωx{displaystyle I'_{x}subset Omega _{x}}
I0(λ)=eλS(x0)∫Iwf[φ(w)]exp(λ∑j=1nμj2wj2)|detφw′(w)|dw.{displaystyle I_{0}(lambda )=e^{lambda S(x^{0})}int _{I_{w}}f[{boldsymbol {varphi }}(w)]exp left(lambda sum _{j=1}^{n}{tfrac {mu _{j}}{2}}w_{j}^{2}right)left|det {boldsymbol {varphi }}_{w}'(w)right|dw.}(10)
![I_0(lambda) = e^{lambda S(x^0)} int_{I_w} f[boldsymbol{varphi}(w)] expleft( lambda sum_{j=1}^n tfrac{mu_j}{2} w_j^2 right) left |detboldsymbol{varphi}_w'(w) right | dw.](https://wikimedia.org/api/rest_v1/media/math/render/svg/e1b524ecff5b68963c862f2b2b85da2571de8042)
Recalling that x0 = φ(0) as well as detφw′(0)=1{displaystyle det {boldsymbol {varphi }}_{w}'(0)=1}
I0(λ)≈f(x0)eλS(x0)∫Rnexp(λ∑j=1nμj2wj2)dw=f(x0)eλS(x0)∏j=1n∫−∞∞e12λμjy2dy.{displaystyle I_{0}(lambda )approx f(x^{0})e^{lambda S(x^{0})}int _{mathbf {R} ^{n}}exp left(lambda sum _{j=1}^{n}{tfrac {mu _{j}}{2}}w_{j}^{2}right)dw=f(x^{0})e^{lambda S(x^{0})}prod _{j=1}^{n}int _{-infty }^{infty }e^{{frac {1}{2}}lambda mu _{j}y^{2}}dy.}(11)
Here, we have substituted the integration region Iw by Rn because both contain the origin, which is a saddle point, hence they are equal up to an exponentially small term.[6] The integrals in the r.h.s. of equation (11) can be expressed as
Ij=∫−∞∞e12λμjy2dy=2∫0∞e−12λ(−μjy)2dy=2∫0∞e−12λ|−μj|2y2exp(2iarg−μj)dy.{displaystyle {mathcal {I}}_{j}=int _{-infty }^{infty }e^{{frac {1}{2}}lambda mu _{j}y^{2}}dy=2int _{0}^{infty }e^{-{frac {1}{2}}lambda left({sqrt {-mu _{j}}}yright)^{2}}dy=2int _{0}^{infty }e^{-{frac {1}{2}}lambda left|{sqrt {-mu _{j}}}right|^{2}y^{2}exp left(2iarg {sqrt {-mu _{j}}}right)}dy.}(12)
From this representation, we conclude that condition (9) must be satisfied in order for the r.h.s. and l.h.s. of equation (12) to coincide. According to assumption 2, ℜ(Sxx″(x0)){displaystyle Re left(S_{xx}''(x^{0})right)}
- Ij=2−μjλ∫0∞e−ξ22dξ=2πλ(−μj)−12.{displaystyle {mathcal {I}}_{j}={frac {2}{{sqrt {-mu _{j}}}{sqrt {lambda }}}}int _{0}^{infty }e^{-{frac {xi ^{2}}{2}}}dxi ={sqrt {frac {2pi }{lambda }}}(-mu _{j})^{-{frac {1}{2}}}.}
Equation (8) can also be written as
I(λ)=(2πλ)n2eλS(x0)(det(−Sxx″(x0)))−12(f(x0)+O(λ−1)),{displaystyle I(lambda )=left({frac {2pi }{lambda }}right)^{frac {n}{2}}e^{lambda S(x^{0})}left(det(-S_{xx}''(x^{0}))right)^{-{frac {1}{2}}}left(f(x^{0})+Oleft(lambda ^{-1}right)right),}(13)
where the branch of
- det(−Sxx″(x0)){displaystyle {sqrt {det left(-S_{xx}''(x^{0})right)}}}
is selected as follows
- (det(−Sxx″(x0)))−12=exp(−i Ind(−Sxx″(x0)))∏j=1n|μj|−12,Ind(−Sxx″(x0))=12∑j=1narg(−μj),|arg(−μj)|<π2.{displaystyle {begin{aligned}left(det left(-S_{xx}''(x^{0})right)right)^{-{frac {1}{2}}}&=exp left(-i{text{ Ind}}left(-S_{xx}''(x^{0})right)right)prod _{j=1}^{n}left|mu _{j}right|^{-{frac {1}{2}}},\{text{Ind}}left(-S_{xx}''(x^{0})right)&={tfrac {1}{2}}sum _{j=1}^{n}arg(-mu _{j}),&&|arg(-mu _{j})|<{tfrac {pi }{2}}.end{aligned}}}
Consider important special cases:
- If S(x) is real valued for real x and x0 in Rn (aka, the multidimensional Laplace method), then[7]
- Ind(−Sxx″(x0))=0.{displaystyle {text{Ind}}left(-S_{xx}''(x^{0})right)=0.}
- Ind(−Sxx″(x0))=0.{displaystyle {text{Ind}}left(-S_{xx}''(x^{0})right)=0.}
- If S(x) is purely imaginary for real x (i.e., ℜ(S(x))=0{displaystyle Re (S(x))=0}
for all x in Rn) and x0 in Rn (aka, the multidimensional stationary phase method),[8] then[9]
- Ind(−Sxx″(x0))=π4sign Sxx″(x0),{displaystyle {text{Ind}}left(-S_{xx}''(x^{0})right)={frac {pi }{4}}{text{sign }}S_{xx}''(x_{0}),}
- Ind(−Sxx″(x0))=π4sign Sxx″(x0),{displaystyle {text{Ind}}left(-S_{xx}''(x^{0})right)={frac {pi }{4}}{text{sign }}S_{xx}''(x_{0}),}
- where sign Sxx″(x0){displaystyle {text{sign }}S_{xx}''(x_{0})}
denotes the signature of matrix Sxx″(x0){displaystyle S_{xx}''(x_{0})}
, which equals to the number of negative eigenvalues minus the number of positive ones. It is noteworthy that in applications of the stationary phase method to the multidimensional WKB approximation in quantum mechanics (as well as in optics), Ind is related to the Maslov index see, e.g., Chaichian & Demichev (2001) and Schulman (2005).
The case of multiple non-degenerate saddle points
If the function S(x) has multiple isolated non-degenerate saddle points, i.e.,
- ∇S(x(k))=0,detSxx″(x(k))≠0,x(k)∈Ωx(k),{displaystyle nabla Sleft(x^{(k)}right)=0,quad det S''_{xx}left(x^{(k)}right)neq 0,quad x^{(k)}in Omega _{x}^{(k)},}
where
- {Ωx(k)}k=1K{displaystyle left{Omega _{x}^{(k)}right}_{k=1}^{K}}
is an open cover of Ωx, then the calculation of the integral asymptotic is reduced to the case of a single saddle point by employing the partition of unity. The partition of unity allows us to construct a set of continuous functions ρk(x) : Ωx → [0, 1], 1 ≤ k ≤ K, such that
- ∑k=1Kρk(x)=1,∀x∈Ωx,ρk(x)=0∀x∈Ωx∖Ωx(k).{displaystyle {begin{aligned}sum _{k=1}^{K}rho _{k}(x)&=1,&&forall xin Omega _{x},\rho _{k}(x)&=0&&forall xin Omega _{x}setminus Omega _{x}^{(k)}.end{aligned}}}
Whence,
- ∫Ix⊂Ωxf(x)eλS(x)dx≡∑k=1K∫Ix⊂Ωxρk(x)f(x)eλS(x)dx.{displaystyle int _{I_{x}subset Omega _{x}}f(x)e^{lambda S(x)}dxequiv sum _{k=1}^{K}int _{I_{x}subset Omega _{x}}rho _{k}(x)f(x)e^{lambda S(x)}dx.}
Therefore as λ → ∞ we have:
- ∑k=1K∫a neighborhood of x(k)f(x)eλS(x)dx=(2πλ)n2∑k=1KeλS(x(k))(det(−Sxx″(x(k))))−12f(x(k)),{displaystyle sum _{k=1}^{K}int _{{text{a neighborhood of }}x^{(k)}}f(x)e^{lambda S(x)}dx=left({frac {2pi }{lambda }}right)^{frac {n}{2}}sum _{k=1}^{K}e^{lambda Sleft(x^{(k)}right)}left(det left(-S_{xx}''left(x^{(k)}right)right)right)^{-{frac {1}{2}}}fleft(x^{(k)}right),}
where equation (13) was utilized at the last stage, and the pre-exponential function f (x) at least must be continuous.
The other cases
When ∇S(z0) = 0 and detSzz″(z0)=0{displaystyle det S''_{zz}(z^{0})=0}
Calculating the asymptotic of
- ∫f(x)eλS(x)dx,{displaystyle int f(x)e^{lambda S(x)}dx,}
when λ → ∞, f (x) is continuous, and S(z) has a degenerate saddle point, is a very rich problem, whose solution heavily relies on the catastrophe theory. Here, the catastrophe theory replaces the Morse lemma, valid only in the non-degenerate case, to transform the function S(z) into one of the multitude of canonical representations. For further details see, e.g., Poston & Stewart (1978) and Fedoryuk (1987).
Integrals with degenerate saddle points naturally appear in many applications including optical caustics and the multidimensional WKB approximation in quantum mechanics.
The other cases such as, e.g., f (x) and/or S(x) are discontinuous or when an extremum of S(x) lies at the integration region's boundary, require special care (see, e.g., Fedoryuk (1987) and Wong (1989)).
Extensions and generalizations
An extension of the steepest descent method is the so-called nonlinear stationary phase/steepest descent method. Here, instead of integrals, one needs to evaluate asymptotically solutions of Riemann–Hilbert factorization problems.
Given a contour C in the complex sphere, a function f defined on that contour and a special point, say infinity, one seeks a function M holomorphic away from the contour C, with prescribed jump across C, and with a given normalization at infinity. If f and hence M are matrices rather than scalars this is a problem that in general does not admit an explicit solution.
An asymptotic evaluation is then possible along the lines of the linear stationary phase/steepest descent method. The idea is to reduce asymptotically the solution of the given Riemann–Hilbert problem to that of a simpler, explicitly solvable, Riemann–Hilbert problem. Cauchy's theorem is used to justify deformations of the jump contour.
The nonlinear stationary phase was introduced by Deift and Zhou in 1993, based on earlier work of the Russian mathematician Alexander Its. A (properly speaking) nonlinear steepest descent method was introduced by Kamvissis, K. McLaughlin and P. Miller in 2003, based on previous work of Lax, Levermore, Deift, Venakides and Zhou. As in the linear case, steepest descent contours solve a min-max problem. In the nonlinear case they turn out to be "S-curves" (defined in a different context back in the 80s by Stahl, Gonchar and Rakhmanov).
The nonlinear stationary phase/steepest descent method has applications to the theory of soliton equations and integrable models, random matrices and combinatorics.
See also
Pearcey integral
Notes
^ A modified version of Lemma 2.1.1 on page 56 in Fedoryuk (1987).
^ Lemma 3.3.2 on page 113 in Fedoryuk (1987)
^ Poston & Stewart (1978), page 54; see also the comment on page 479 in Wong (1989).
^ Fedoryuk (1987), pages 417-420.
^ This conclusion follows from a comparison between the final asymptotic for I0(λ), given by equation (8), and a simple estimate for the discarded integral I1(λ).
^ This is justified by comparing the integral asymptotic over Rn [see equation (8)] with a simple estimate for the altered part.
^ See equation (4.4.9) on page 125 in Fedoryuk (1987)
^ Rigorously speaking, this case cannot be inferred from equation (8) because the second assumption, utilized in the derivation, is violated. To include the discussed case of a purely imaginary phase function, condition (9) should be replaced by |arg−μj|⩽π4.{displaystyle left|arg {sqrt {-mu _{j}}}right|leqslant {tfrac {pi }{4}}.}
^ See equation (2.2.6') on page 186 in Fedoryuk (1987)
References
Chaichian, M.; Demichev, A. (2001), Path Integrals in Physics Volume 1: Stochastic Process and Quantum Mechanics, Taylor & Francis, p. 174, ISBN 075030801X.mw-parser-output cite.citation{font-style:inherit}.mw-parser-output q{quotes:"""""""'""'"}.mw-parser-output code.cs1-code{color:inherit;background:inherit;border:inherit;padding:inherit}.mw-parser-output .cs1-lock-free a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/6/65/Lock-green.svg/9px-Lock-green.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-lock-limited a,.mw-parser-output .cs1-lock-registration a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/d/d6/Lock-gray-alt-2.svg/9px-Lock-gray-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-lock-subscription a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/a/aa/Lock-red-alt-2.svg/9px-Lock-red-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration{color:#555}.mw-parser-output .cs1-subscription span,.mw-parser-output .cs1-registration span{border-bottom:1px dotted;cursor:help}.mw-parser-output .cs1-hidden-error{display:none;font-size:100%}.mw-parser-output .cs1-visible-error{font-size:100%}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration,.mw-parser-output .cs1-format{font-size:95%}.mw-parser-output .cs1-kern-left,.mw-parser-output .cs1-kern-wl-left{padding-left:0.2em}.mw-parser-output .cs1-kern-right,.mw-parser-output .cs1-kern-wl-right{padding-right:0.2em}
Debye, P. (1909), "Näherungsformeln für die Zylinderfunktionen für große Werte des Arguments und unbeschränkt veränderliche Werte des Index", Mathematische Annalen, 67 (4): 535–558, doi:10.1007/BF01450097 English translation in Debye, Peter J. W. (1954), The collected papers of Peter J. W. Debye, Interscience Publishers, Inc., New York, ISBN 978-0-918024-58-9, MR 0063975
Deift, P.; Zhou, X. (1993), "A steepest descent method for oscillatory Riemann-Hilbert problems. Asymptotics for the MKdV equation", Ann. of Math., The Annals of Mathematics, Vol. 137, No. 2, 137 (2), pp. 295–368, arXiv:math/9201261, doi:10.2307/2946540, JSTOR 2946540.
Erdelyi, A. (1956), Asymptotic Expansions, Dover.
Fedoryuk, M V (2001) [1994], "Saddle_point_method", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4.
Fedoryuk, M. V. (1987), Asymptotic: Integrals and Series, Nauka, Moscow [in Russian].
Kamvissis, S.; McLaughlin, K. T.-R.; Miller, P. (2003), "Semiclassical Soliton Ensembles for the Focusing Nonlinear Schrödinger Equation", Annals of Mathematics Studies, Princeton University Press, 154.
Riemann, B. (1863), Sullo svolgimento del quoziente di due serie ipergeometriche in frazione continua infinita (Unpublished note, reproduced in Riemann's collected papers.)
Siegel, C. L. (1932), "Über Riemanns Nachlaß zur analytischen Zahlentheorie", Quellen Studien zur Geschichte der Math. Astron. und Phys. Abt. B: Studien 2: 45–80 Reprinted in Gesammelte Abhandlungen, Vol. 1. Berlin: Springer-Verlag, 1966.
Poston, T.; Stewart, I. (1978), Catastrophe Theory and Its Applications, Pitman.
Schulman, L. S. (2005), "Ch. 17: The Phase of the Semiclassical Amplitude", Techniques and Applications of Path Integration, Dover, ISBN 0486445283
Wong, R. (1989), Asymptotic approximations of integrals, Academic Press.
