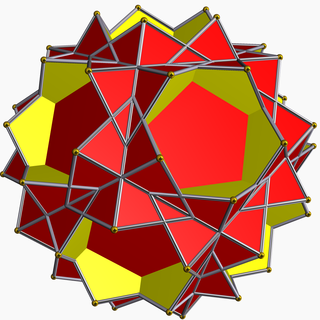
Small stellated truncated dodecahedron











































Small stellated truncated dodecahedron

Small stellated truncated dodecahedron.png
Type
Uniform star polyhedron
Elements
F = 24, E = 90
V = 60 (χ = −6)
Faces by sides 12{5}+12{10/3}
Wythoff symbol 2 5 | 5/3
2 5/4 | 5/3
Symmetry group Ih, [5,3], *532
Index references
U58, C74, W97
Dual polyhedron
Great pentakis dodecahedron
Vertex figure
Small stellated truncated dodecahedron vertfig.png
5.10/3.10/3
Bowers acronym Quit Sissid

In geometry, the small stellated truncated dodecahedron or quasitruncated small stellated dodecahedron is a nonconvex uniform polyhedron, indexed as U58. It is given a Schläfli symbol t{5/3,5}, and Coxeter diagram CDel node 1.pngCDel 5-3.pngCDel node 1.pngCDel 5.pngCDel node.png.


It has 12 pentagons and 12 decagrams, {10/3} faces.



Related polyhedra


It shares its vertex arrangement with three other uniform polyhedra: the convex rhombicosidodecahedron, the small dodecicosidodecahedron and the small rhombidodecahedron.


It also has the same vertex arrangement as the uniform compounds of 6 or 12 pentagrammic prisms.














Small rhombicosidodecahedron.png
Rhombicosidodecahedron
Small dodecicosidodecahedron.png
Small dodecicosidodecahedron
Small rhombidodecahedron.png
Small rhombidodecahedron

Small stellated truncated dodecahedron.png
Small stellated truncated dodecahedron
UC36-6 pentagrammic prisms.png
Compound of six pentagrammic prisms
UC37-12 pentagrammic prisms.png
Compound of twelve pentagrammic prisms


See also


  • List of uniform polyhedra


External links


  • Weisstein, Eric W. "Small stellated truncated dodecahedron". MathWorld..mw-parser-output cite.citation{font-style:inherit}.mw-parser-output .citation q{quotes:"""""""'""'"}.mw-parser-output .citation .cs1-lock-free a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/6/65/Lock-green.svg/9px-Lock-green.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .citation .cs1-lock-limited a,.mw-parser-output .citation .cs1-lock-registration a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/d/d6/Lock-gray-alt-2.svg/9px-Lock-gray-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .citation .cs1-lock-subscription a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/a/aa/Lock-red-alt-2.svg/9px-Lock-red-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration{color:#555}.mw-parser-output .cs1-subscription span,.mw-parser-output .cs1-registration span{border-bottom:1px dotted;cursor:help}.mw-parser-output .cs1-ws-icon a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/4/4c/Wikisource-logo.svg/12px-Wikisource-logo.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output code.cs1-code{color:inherit;background:inherit;border:inherit;padding:inherit}.mw-parser-output .cs1-hidden-error{display:none;font-size:100%}.mw-parser-output .cs1-visible-error{font-size:100%}.mw-parser-output .cs1-maint{display:none;color:#33aa33;margin-left:0.3em}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration,.mw-parser-output .cs1-format{font-size:95%}.mw-parser-output .cs1-kern-left,.mw-parser-output .cs1-kern-wl-left{padding-left:0.2em}.mw-parser-output .cs1-kern-right,.mw-parser-output .cs1-kern-wl-right{padding-right:0.2em}









-

Popular posts from this blog

Italian cuisine

Image
"Italian restaurant" redirects here. For the television series, see Italian Restaurant. Some typical Italian gastronomic products in a window display in Imola Pizza is one of the world's most popular foods and a common fast food item Part of a series on the Culture of Italy History People Languages Traditions Mythology and folklore Mythology folklore Cuisine Festivals Religion Art Literature Music and performing arts Music Media Television Cinema Sport Monuments World Heritage Sites Symbols Flag Coat of arms Italy portal v t e Italian cuisine History Ancient Roman cuisine Medieval cuisine Early modern cuisine Contemporary cuisine Regional cuisines Apulian cuisine Lombard cuisine Neapolitan cuisine Roman cuisine Sicilian cuisine Venetian cuisine Cuisine of Abruzzo Cuisine of Sardinia Lists Chefs Dishes Pas...
Read more

Bulgarian cuisine

Image
Part of a series on Bulgarians .mw-parser-output .nobold{font-weight:normal} българи Culture Literature Music Art Cinema Names Cuisine Dances Costume Sport Public holidays in Bulgaria By country Albania Australia Canada Czechoslovakia Greece New Zealand Romania Serbia South America Turkey Ukraine United States Bulgarian citizens France Germany Hungary Italy Lebanon Lithuania Macedonia Spain United Kingdom Subgroups Anatolian Balkanian Banat Bulgarians Bessarabian Bulgarian Dobrujans Macedonian Ruptsi Balkandzhii Pomaks (Bulgarian Muslims) Thracian Shopi/Torlaks Şchei Religion Bulgarian Orthodox Church Islam Catholic Church Protestant denominations Language Bulgarian Dialects Banat Bulgarian Other List of Bulgarians People of Bulgarian descent v t e Tarator is a cold soup made of yogurt, water, minced cucumber, dill, garlic, and sunflower or olive oil (Chips are...
Read more

Carrot

Image
Root vegetable, usually orange in color This article is about the cultivated vegetable. For other uses, see Carrot (disambiguation). Carrot Scientific classification Kingdom: Plantae Clade : Angiosperms Clade : Eudicots Clade : Asterids Order: Apiales Family: Apiaceae Genus: Daucus Species: D. carota Subspecies: D. c. subsp. sativus Trinomial name Daucus carota subsp. sativus (Hoffm.) Schübl. & G. Martens The carrot ( Daucus carota subsp. sativus ) is a root vegetable, usually orange in colour, though purple, black, red, white, and yellow cultivars exist. [1] Carrots are a domesticated form of the wild carrot, Daucus carota , native to Europe and southwestern Asia. The plant probably originated in Persia and was originally cultivated for its leaves and seeds. The most commonly eaten part of the plant is the taproot, although the stems and leaves are eaten as well. The domestic carrot ha...
Read more