Polytope compound
A polyhedral compound is a figure that is composed of several polyhedra sharing a common centre. They are the three-dimensional analogs of polygonal compounds such as the hexagram.
The outer vertices of a compound can be connected to form a convex polyhedron called the convex hull. The compound is a facetting of the convex hull.
Another convex polyhedron is formed by the small central space common to all members of the compound. This polyhedron can be used as the core for a set of stellations.
Contents
1 Regular compounds
2 Dual compounds
3 Uniform compounds
4 Other compounds
5 4-polytope compounds
5.1 Compounds with regular star 4-polytopes
5.2 Compounds with duals
6 Group theory
7 Compounds of tilings
8 Footnotes
9 External links
10 References
Regular compounds
A regular polyhedron compound can be defined as a compound which, like a regular polyhedron, is vertex-transitive, edge-transitive, and face-transitive. There are five regular compounds of polyhedra.
| Components Coxeter symbol | Picture | Spherical | Convex hull (Core) | Symmetry | Subgroup restricting to one constituent | Dual |
|---|---|---|---|---|---|---|
Two tetrahedra {4,3}[2{3,3}]{3,4} |  |  | Cube (Octahedron) | *432 [4,3] Oh | *332 [3,3] Td | Self-dual |
Five tetrahedra {5,3}[5{3,3}]{3,5} |  |  | Dodecahedron (Icosahedron) | 532 [5,3]+ I | 332 [3,3]+ T | enantiomorph chiral twin |
Ten tetrahedra 2{5,3}[10{3,3}]2{3,5} |  |  | Dodecahedron (Icosahedron) | *532 [5,3] Ih | 332 [3,3] T | Self-dual |
Five cubes 2{5,3}[5{4,3}] | 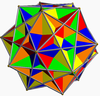 |  | Dodecahedron (Rhombic triacontahedron) | *532 [5,3] Ih | 3*2 [3,3] Th | Five octahedra |
Five octahedra [5{3,4}]2{3,5} |  |  | Icosidodecahedron (Icosahedron) | *532 [5,3] Ih | 3*2 [3,3] Th | Five cubes |
Best known is the compound of two tetrahedra, often called the stella octangula, a name given to it by Kepler. The vertices of the two tetrahedra define a cube and the intersection of the two an octahedron, which shares the same face-planes as the compound. Thus it is a stellation of the octahedron, and in fact, the only finite stellation thereof.
The stella octangula can also be regarded as a dual-regular compound.
The compound of five tetrahedra comes in two enantiomorphic versions, which together make up the compound of 10 tetrahedra. Each of the tetrahedral compounds is self-dual, and the compound of 5 cubes is dual to the compound of 5 octahedra.
Coxeter's notation for regular compounds is given in the table above, incorporating Schläfli symbols. The material inside the square brackets, [d{p,q}], denotes the components of the compound: d separate {p,q}'s. The material before the square brackets denotes the vertex arrangement of the compound: c{m,n}[d{p,q}] is a compound of d {p,q}'s sharing the vertices of an {m,n} counted c times. The material after the square brackets denotes the facet arrangement of the compound: [d{p,q}]e{s,t} is a compound of d {p,q}'s sharing the faces of {s,t} counted e times. These may be combined: thus c{m,n}[d{p,q}]e{s,t} is a compound of d {p,q}'s sharing the vertices of {m,n} counted c times and the faces of {s,t} counted e times. This notation can be generalised to compounds in any number of dimensions.[1]
Dual compounds
.mw-parser-output .tmulti .thumbinner{display:flex;flex-direction:column}.mw-parser-output .tmulti .trow{display:flex;flex-direction:row;clear:left;flex-wrap:wrap;width:100%;box-sizing:border-box}.mw-parser-output .tmulti .tsingle{margin:1px;float:left}.mw-parser-output .tmulti .theader{clear:both;font-weight:bold;text-align:center;align-self:center;background-color:transparent;width:100%}.mw-parser-output .tmulti .thumbcaption{text-align:left;background-color:transparent}.mw-parser-output .tmulti .text-align-left{text-align:left}.mw-parser-output .tmulti .text-align-right{text-align:right}.mw-parser-output .tmulti .text-align-center{text-align:center}@media all and (max-width:720px){.mw-parser-output .tmulti .thumbinner{width:100%!important;box-sizing:border-box;max-width:none!important;align-items:center}.mw-parser-output .tmulti .trow{justify-content:center}.mw-parser-output .tmulti .tsingle{float:none!important;max-width:100%!important;box-sizing:border-box;text-align:center}.mw-parser-output .tmulti .thumbcaption{text-align:center}}

Truncated tetrahedron (light) and triakis tetrahedron (dark)

Snub cube (light) and pentagonal icositetrahedron (dark)

Icosidodecahedron (light) and rhombic triacontahedron (dark)
A dual compound is composed of a polyhedron and its dual, arranged reciprocally about a common intersphere or midsphere, such that the edge of one polyhedron intersects the dual edge of the dual polyhedron. There are five such compounds of the regular polyhedra.
The core is the rectification of both solids. The hull is the dual of this rectification, and its faces have the intersecting edges of the two solids as diagonals. For the convex solids this is the convex hull.
| Components | Picture | Hull | Core | Symmetry |
|---|---|---|---|---|
| Two tetrahedra (Compound of two tetrahedra, stellated octahedron) |  | Cube | Octahedron | *432 [4,3] Oh |
Cube, Octahedron (Compound of cube and octahedron) |  | Rhombic dodecahedron | Cuboctahedron | *432 [4,3] Oh |
Dodecahedron, Icosahedron (Compound of dodecahedron and icosahedron) |  | Rhombic triacontahedron | Icosidodecahedron | *532 [5,3] Ih |
Small stellated dodecahedron, Great dodecahedron (Compound of sD and gD) |  | Medial rhombic triacontahedron (Convex: Icosahedron) | Dodecadodecahedron (Convex: Dodecahedron) | *532 [5,3] Ih |
Great icosahedron, Great stellated dodecahedron (Compound of gI and gsD) |  | Great rhombic triacontahedron (Convex: Dodecahedron) | Great icosidodecahedron (Convex: Icosahedron) | *532 [5,3] Ih |
The tetrahedron is self-dual, so the dual compound of a tetrahedron with its dual is the regular stellated octahedron.
The octahedral and icosahedral dual compounds are the first stellations of the cuboctahedron and icosidodecahedron, respectively.
Uniform compounds
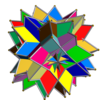
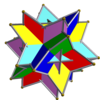
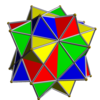
In 1976 John Skilling published Uniform Compounds of Uniform Polyhedra which enumerated 75 compounds (including 6 as infinite prismatic sets of compounds, #20-#25) made from uniform polyhedra with rotational symmetry. (Every vertex is vertex-transitive and every vertex is transitive with every other vertex.) This list includes the five regular compounds above. [1]
The 75 uniform compounds are listed in the Table below. Most are shown singularly colored by each polyhedron element. Some chiral pairs of face groups are colored by symmetry of the faces within each polyhedron.
- 1-19: Miscellaneous (4,5,6,9,17 are the 5 regular compounds)
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |
- 20-25: Prism symmetry embedded in prism symmetry,
 |  |  |  |  |  |
- 26-45: Prism symmetry embedded in octahedral or icosahedral symmetry,
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |
- 46-67: Tetrahedral symmetry embedded in octahedral or icosahedral symmetry,
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |
- 68-75: enantiomorph pairs
 |  |  |  |  |  |
 |  |
Other compounds
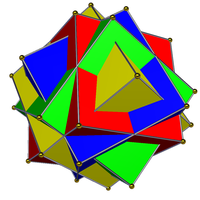 | 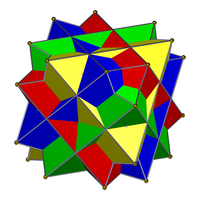 |
| These compounds, of four cubes, and (dual) four octahedra, are neither regular compounds, nor dual compounds, nor uniform compounds. | |
- Compound of three octahedra
- Compound of four cubes
Two polyhedra that are compounds but have their elements rigidly locked into place are the small complex icosidodecahedron (compound of icosahedron and great dodecahedron) and the great complex icosidodecahedron (compound of small stellated dodecahedron and great icosahedron). If the definition of a uniform polyhedron is generalised they are uniform.
The section for entianomorphic pairs in Skilling's list does not contain the compound of two great snub dodecicosidodecahedra, as the pentagram faces would coincide. Removing the coincident faces results in the compound of twenty octahedra.
4-polytope compounds
 |  |
| 75 {4,3,3} | 75 {3,3,4} |
|---|
In 4-dimensions, there are a large number of regular compounds of regular polytopes. Coxeter lists a few of these in his book Regular Polytopes:[2]
Self-duals:
| Compound | Constituent | Symmetry |
|---|---|---|
| 120 5-cell | 5-cell | [5,3,3], order 14400 |
| 5 24-cell | 24-cell | [5,3,3], order 14400 |
Dual pairs:
| Compound 1 | Compound 2 | Symmetry |
|---|---|---|
| 3 16-cells[3] | 3 tesseracts | [3,4,3], order 1152 |
| 15 16-cells | 15 tesseracts | [5,3,3], order 14400 |
| 75 16-cells | 75 tesseracts | [5,3,3], order 14400 |
| 300 16-cells | 300 tesseracts | [5,3,3]+, order 7200 |
| 600 16-cells | 600 tesseracts | [5,3,3], order 14400 |
| 25 24-cells | 25 24-cells | [5,3,3], order 14400 |
Uniform compounds and duals with convex 4-polytopes:
| Compound 1 Vertex-transitive | Compound 2 Cell-transitive | Symmetry |
|---|---|---|
| 2 16-cells[4] | 2 tesseracts | [4,3,3], order 384 |
| 100 24-cell | 100 24-cell | [5,3,3]+, order 7200 |
| 200 24-cell | 200 24-cell | [5,3,3], order 14400 |
| 5 600-cell | 5 120-cell | [5,3,3]+, order 7200 |
| 10 600-cell | 10 120-cell | [5,3,3], order 14400 |
Compounds with regular star 4-polytopes
Self-dual star compounds:
| Compound | Symmetry |
|---|---|
| 5 {5,5/2,5} | [5,3,3]+, order 7200 |
| 10 {5,5/2,5} | [5,3,3], order 14400 |
| 5 {5/2,5,5/2} | [5,3,3]+, order 7200 |
| 10 {5/2,5,5/2} | [5,3,3], order 14400 |
Dual pairs of compound stars:
| Compound 1 | Compound 2 | Symmetry |
|---|---|---|
| 5 {3,5,5/2} | 5 {5/2,5,3} | [5,3,3]+, order 7200 |
| 10 {3,5,5/2} | 10 {5/2,5,3} | [5,3,3], order 14400 |
| 5 {5,5/2,3} | 5 {3,5/2,5} | [5,3,3]+, order 7200 |
| 10 {5,5/2,3} | 10 {3,5/2,5} | [5,3,3], order 14400 |
| 5 {5/2,3,5} | 5 {5,3,5/2} | [5,3,3]+, order 7200 |
| 10 {5/2,3,5} | 10 {5,3,5/2} | [5,3,3], order 14400 |
Uniform compound stars and duals:
| Compound 1 Vertex-transitive | Compound 2 Cell-transitive | Symmetry |
|---|---|---|
| 5 {3,3,5/2} | 5 {5/2,3,3} | [5,3,3]+, order 7200 |
| 10 {3,3,5/2} | 10 {5/2,3,3} | [5,3,3], order 14400 |
Compounds with duals
Dual positions:
| Compound | Constituent | Symmetry |
|---|---|---|
| 2 5-cell | 5-cell | [[3,3,3]], order 240 |
| 2 24-cell | 24-cell | [[3,4,3]], order 2304 |
| 1 tesseract, 1 16-cell | tesseract, 16-cell | |
| 1 120-cell, 1 600-cell | 120-cell, 600-cell | |
| 2 great 120-cell | great 120-cell | |
| 2 grand stellated 120-cell | grand stellated 120-cell | |
| 1 icosahedral 120-cell, 1 small stellated 120-cell | icosahedral 120-cell, small stellated 120-cell | |
| 1 grand 120-cell, 1 great stellated 120-cell | grand 120-cell, great stellated 120-cell | |
| 1 great grand 120-cell, 1 great icosahedral 120-cell | great grand 120-cell, great icosahedral 120-cell | |
| 1 great grand stellated 120-cell, 1 grand 600-cell | great grand stellated 120-cell, grand 600-cell |
Only the first two of these dual compounds are also regular.
Group theory
In terms of group theory, if G is the symmetry group of a polyhedral compound, and the group acts transitively on the polyhedra (so that each polyhedron can be sent to any of the others, as in uniform compounds), then if H is the stabilizer of a single chosen polyhedron, the polyhedra can be identified with the orbit space G/H – the coset gH corresponds to which polyhedron g sends the chosen polyhedron to.
Compounds of tilings
There are eighteen two-parameter families of regular compound tessellations of the Euclidean plane. In the hyperbolic plane, five one-parameter families and seventeen isolated cases are known, but the completeness of this listing has not been enumerated.
The Euclidean and hyperbolic compound families 2 {p,p} (4 ≤ p ≤ ∞, p an integer) are analogous to the spherical stella octangula, 2 {3,3}.
| Self-dual | Duals | Self-dual | |
|---|---|---|---|
| 2 {4,4} | 2 {6,3} | 2 {3,6} | 2 {∞,∞} |
 |  |  |  |
| 3 {6,3} | 3 {3,6} | 3 {∞,∞} | |
 |  |  | |
A known family of regular Euclidean compound honeycombs in five or more dimensions is an infinite family of compounds of hypercubic honeycombs, all sharing vertices and faces with another hypercubic honeycomb. This compound can have any number of hypercubic honeycombs.
There are also dual-regular tiling compounds. A simple example is the E2 compound of a hexagonal tiling and its dual triangular tiling, which shares its edges with the deltoidal trihexagonal tiling. The Euclidean compounds of two hypercubic honeycombs are both regular and dual-regular.
Footnotes
^ Coxeter, Harold Scott MacDonald (1973) [1948]. Regular Polytopes (Third ed.). Dover Publications. p. 48. ISBN 0-486-61480-8. OCLC 798003..mw-parser-output cite.citation{font-style:inherit}.mw-parser-output .citation q{quotes:"""""""'""'"}.mw-parser-output .citation .cs1-lock-free a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/6/65/Lock-green.svg/9px-Lock-green.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .citation .cs1-lock-limited a,.mw-parser-output .citation .cs1-lock-registration a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/d/d6/Lock-gray-alt-2.svg/9px-Lock-gray-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .citation .cs1-lock-subscription a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/a/aa/Lock-red-alt-2.svg/9px-Lock-red-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration{color:#555}.mw-parser-output .cs1-subscription span,.mw-parser-output .cs1-registration span{border-bottom:1px dotted;cursor:help}.mw-parser-output .cs1-ws-icon a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/4/4c/Wikisource-logo.svg/12px-Wikisource-logo.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output code.cs1-code{color:inherit;background:inherit;border:inherit;padding:inherit}.mw-parser-output .cs1-hidden-error{display:none;font-size:100%}.mw-parser-output .cs1-visible-error{font-size:100%}.mw-parser-output .cs1-maint{display:none;color:#33aa33;margin-left:0.3em}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration,.mw-parser-output .cs1-format{font-size:95%}.mw-parser-output .cs1-kern-left,.mw-parser-output .cs1-kern-wl-left{padding-left:0.2em}.mw-parser-output .cs1-kern-right,.mw-parser-output .cs1-kern-wl-right{padding-right:0.2em}
^ Regular polytopes, Table VII, p. 305
^ Klitzing, Richard. "Uniform compound stellated icositetrachoron".
^ Klitzing, Richard. "Uniform compound demidistesseract".
External links
- MathWorld: Polyhedron Compound
Compound polyhedra – from Virtual Reality Polyhedra
- Uniform Compounds of Uniform Polyhedra
- Skilling's 75 Uniform Compounds of Uniform Polyhedra
- Skilling's Uniform Compounds of Uniform Polyhedra
- Polyhedral Compounds
- http://users.skynet.be/polyhedra.fleurent/Compounds_2/Compounds_2.htm
- Compound of Small Stellated Dodecahedron and Great Dodecahedron {5/2,5}+{5,5/2}
Klitzing, Richard. "Compound polytopes".
References
Skilling, John (1976), "Uniform Compounds of Uniform Polyhedra", Mathematical Proceedings of the Cambridge Philosophical Society, 79: 447–457, doi:10.1017/S0305004100052440, MR 0397554.
Cromwell, Peter R. (1997), Polyhedra, Cambridge.
Wenninger, Magnus (1983), Dual Models, Cambridge, England: Cambridge University Press, pp. 51–53.
Harman, Michael G. (1974), Polyhedral Compounds, unpublished manuscript.
Hess, Edmund (1876), "Zugleich Gleicheckigen und Gleichflächigen Polyeder", Schriften der Gesellschaft zur Berörderung der Gasammten Naturwissenschaften zu Marburg, 11: 5–97.
Pacioli, Luca (1509), De Divina Proportione.
Regular Polytopes, (3rd edition, 1973), Dover edition,
ISBN 0-486-61480-8
Anthony Pugh (1976). Polyhedra: A visual approach. California: University of California Press Berkeley. ISBN 0-520-03056-7. p. 87 Five regular compounds