Rhombicosidodecahedron
| Rhombicosidodecahedron | |
|---|---|
 (Click here for rotating model) | |
| Type | Archimedean solid Uniform polyhedron |
| Elements | F = 62, E = 120, V = 60 (χ = 2) |
| Faces by sides | 20{3}+30{4}+12{5} |
| Conway notation | eD or aaD |
| Schläfli symbols | rr{5,3} or r{53}{displaystyle r{begin{Bmatrix}5\3end{Bmatrix}}} |
| t0,2{5,3} | |
| Wythoff symbol | 3 5 | 2 |
| Coxeter diagram | |
| Symmetry group | Ih, H3, [5,3], (*532), order 120 |
| Rotation group | I, [5,3]+, (532), order 60 |
| Dihedral angle | 3-4: 159°05′41″ (159.09°) 4-5: 148°16′57″ (148.28°) |
| References | U27, C30, W14 |
| Properties | Semiregular convex |
 Colored faces |  3.4.5.4 (Vertex figure) |
 Deltoidal hexecontahedron (dual polyhedron) |  Net |
In geometry, the rhombicosidodecahedron, is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed of two or more types of regular polygon faces.
It has 20 regular triangular faces, 30 square faces, 12 regular pentagonal faces, 60 vertices, and 120 edges.
Contents
1 Names
2 Geometric relations
3 Cartesian coordinates
4 Orthogonal projections
5 Spherical tiling
6 Related polyhedra
6.1 Symmetry mutations
6.2 Johnson solids
6.3 Vertex arrangement
7 Rhombicosidodecahedral graph
8 See also
9 Notes
10 References
11 External links
Names
.mw-parser-output .tmulti .thumbinner{display:flex;flex-direction:column}.mw-parser-output .tmulti .trow{display:flex;flex-direction:row;clear:left;flex-wrap:wrap;width:100%;box-sizing:border-box}.mw-parser-output .tmulti .tsingle{margin:1px;float:left}.mw-parser-output .tmulti .theader{clear:both;font-weight:bold;text-align:center;align-self:center;background-color:transparent;width:100%}.mw-parser-output .tmulti .thumbcaption{text-align:left;background-color:transparent}.mw-parser-output .tmulti .text-align-left{text-align:left}.mw-parser-output .tmulti .text-align-right{text-align:right}.mw-parser-output .tmulti .text-align-center{text-align:center}@media all and (max-width:720px){.mw-parser-output .tmulti .thumbinner{width:100%!important;box-sizing:border-box;max-width:none!important;align-items:center}.mw-parser-output .tmulti .trow{justify-content:center}.mw-parser-output .tmulti .tsingle{float:none!important;max-width:100%!important;box-sizing:border-box;text-align:center}.mw-parser-output .tmulti .thumbcaption{text-align:center}}
Johannes Kepler in Harmonices Mundi (1618) named this polyhedron a rhombicosidodecahedron, being short for truncated icosidodecahedral rhombus, with icosidodecahedral rhombus being his name for a rhombic triacontahedron.[1] There are different truncations of a rhombic triacontahedron into a topological rhombicosidodecahedron: Prominently its rectification (left), the one that creates the uniform solid (center), and the core of the compound with its dual (right).
It can also be called an expanded or cantellated dodecahedron or icosahedron, from truncation operations on either uniform polyhedron.
Geometric relations
If you expand an icosahedron by moving the faces away from the origin the right amount, without changing the orientation or size of the faces, and do the same to its dual dodecahedron, and patch the square holes in the result, you get a rhombicosidodecahedron. Therefore, it has the same number of triangles as an icosahedron and the same number of pentagons as a dodecahedron, with a square for each edge of either.
The rhombicosidodecahedron shares the vertex arrangement with the small stellated truncated dodecahedron, and with the uniform compounds of six or twelve pentagrammic prisms.
The Zometool kits for making geodesic domes and other polyhedra use slotted balls as connectors. The balls are "expanded" rhombicosidodecahedra, with the squares replaced by rectangles. The expansion is chosen so that the resulting rectangles are golden rectangles.
Twelve of the 92 Johnson solids are derived from the rhombicosidodecahedron, four of them by rotation of one or more pentagonal cupolae: the gyrate, parabigyrate, metabigyrate, and trigyrate rhombicosidodecahedron. Eight more can be constructed by removing up to three cupolae, sometimes also rotating one or more of the other cupolae.
Cartesian coordinates
Cartesian coordinates for the vertices of a rhombicosidodecahedron with an edge length of 2 centered at the origin are all even permutations of:[2]
- (±1, ±1, ±φ3),
- (±φ2, ±φ, ±2φ),
- (±(2+φ), 0, ±φ2),
where φ = 1 + √5/2 is the golden ratio. Therefore, the circumradius of this rhombicosidodecahedron is the common distance of these points from the origin, namely √φ6+2 = √8φ+7 for edge length 2. For unit edge length, R must be halved, giving
R = √8φ+7/2 = √11+4√5/2 ≈ 2.233.
Orthogonal projections
The rhombicosidodecahedron has six special orthogonal projections, centered, on a vertex, on two types of edges, and three types of faces: triangles, squares, and pentagons. The last two correspond to the A2 and H2Coxeter planes.
| Centered by | Vertex | Edge 3-4 | Edge 5-4 | Face Square | Face Triangle | Face Pentagon |
|---|---|---|---|---|---|---|
| Solid |  |  |  | |||
| Wireframe |  |  |  |  |  |  |
| Projective symmetry | [2] | [2] | [2] | [2] | [6] | [10] |
| Dual image |  |  |  |  |  |  |
Spherical tiling
The rhombicosidodecahedron can also be represented as a spherical tiling, and projected onto the plane via a stereographic projection. This projection is conformal, preserving angles but not areas or lengths. Straight lines on the sphere are projected as circular arcs on the plane.
 |  Pentagon-centered |  Triangle-centered |  Square-centered |
Orthographic projection | Stereographic projections | ||
|---|---|---|---|
Related polyhedra

Expansion of either a dodecahedron or an icosahedron creates a rhombicosidodecahedron.

A version with golden rectangles is used as vertex element of the construction set Zometool.[3]
| Family of uniform icosahedral polyhedra | |||||||
|---|---|---|---|---|---|---|---|
Symmetry: [5,3], (*532) | [5,3]+, (532) | ||||||
 |  |  |  |  |  |  |  |
{5,3} | t{5,3} | r{5,3} | t{3,5} | {3,5} | rr{5,3} | tr{5,3} | sr{5,3} |
| Duals to uniform polyhedra | |||||||
 |  |  |  |  |  | ||
V5.5.5 | V3.10.10 | V3.5.3.5 | V5.6.6 | V3.3.3.3.3 | V3.4.5.4 | V4.6.10 | V3.3.3.3.5 |
Symmetry mutations
This polyhedron is topologically related as a part of a sequence of cantellated polyhedra with vertex figure (3.4.n.4), which continues as tilings of the hyperbolic plane. These vertex-transitive figures have (*n32) reflectional symmetry.
| *n32 symmetry mutation of expanded tilings: 3.4.n.4 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Symmetry *n32 [n,3] | Spherical | Euclid. | Compact hyperb. | Paracomp. | ||||
| *232 [2,3] | *332 [3,3] | *432 [4,3] | *532 [5,3] | *632 [6,3] | *732 [7,3] | *832 [8,3]... | *∞32 [∞,3] | |
| Figure |  |  |  |  |  |  |  | |
Config. | 3.4.2.4 | 3.4.3.4 | 3.4.4.4 | 3.4.5.4 | 3.4.6.4 | 3.4.7.4 | 3.4.8.4 | 3.4.∞.4 |
Johnson solids
There are 13 related Johnson solids, 5 by diminishment, and 8 including gyrations:
J5  | 76  | 80  | 81  | 83  |
72  | 73  | 74  | 75  |
77  | 78  | 79  | 82  |
Vertex arrangement
The rhombicosidodecahedron shares its vertex arrangement with three nonconvex uniform polyhedra: the small stellated truncated dodecahedron, the small dodecicosidodecahedron (having the triangular and pentagonal faces in common), and the small rhombidodecahedron (having the square faces in common).
It also shares its vertex arrangement with the uniform compounds of six or twelve pentagrammic prisms.
 Rhombicosidodecahedron |  Small dodecicosidodecahedron |  Small rhombidodecahedron |
 Small stellated truncated dodecahedron |  Compound of six pentagrammic prisms |  Compound of twelve pentagrammic prisms |
Rhombicosidodecahedral graph
| Rhombicosidodecahedral graph | |
|---|---|
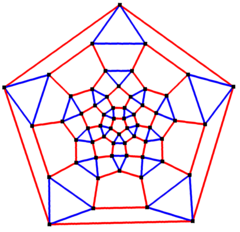 Pentagon centered Schlegel diagram | |
| Vertices | 60 |
| Edges | 120 |
| Automorphisms | 120 |
| Properties | Quartic graph, Hamiltonian, regular |
| Table of graphs and parameters | |
In the mathematical field of graph theory, a rhombicosidodecahedral graph is the graph of vertices and edges of the rhombicosidodecahedron, one of the Archimedean solids. It has 60 vertices and 120 edges, and is a quartic graph Archimedean graph.[4]

Square centered Schlegel diagram
See also
- Truncated rhombicosidodecahedron
Notes
^ Harmonies Of The World by Johannes Kepler, Translated into English with an introduction and notes by E. J. Aiton, A. M. Duncan, "J. V. Field, 1997, .mw-parser-output cite.citation{font-style:inherit}.mw-parser-output .citation q{quotes:"""""""'""'"}.mw-parser-output .citation .cs1-lock-free a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/6/65/Lock-green.svg/9px-Lock-green.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .citation .cs1-lock-limited a,.mw-parser-output .citation .cs1-lock-registration a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/d/d6/Lock-gray-alt-2.svg/9px-Lock-gray-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .citation .cs1-lock-subscription a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/a/aa/Lock-red-alt-2.svg/9px-Lock-red-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration{color:#555}.mw-parser-output .cs1-subscription span,.mw-parser-output .cs1-registration span{border-bottom:1px dotted;cursor:help}.mw-parser-output .cs1-ws-icon a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/4/4c/Wikisource-logo.svg/12px-Wikisource-logo.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output code.cs1-code{color:inherit;background:inherit;border:inherit;padding:inherit}.mw-parser-output .cs1-hidden-error{display:none;font-size:100%}.mw-parser-output .cs1-visible-error{font-size:100%}.mw-parser-output .cs1-maint{display:none;color:#33aa33;margin-left:0.3em}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration,.mw-parser-output .cs1-format{font-size:95%}.mw-parser-output .cs1-kern-left,.mw-parser-output .cs1-kern-wl-left{padding-left:0.2em}.mw-parser-output .cs1-kern-right,.mw-parser-output .cs1-kern-wl-right{padding-right:0.2em}
ISBN 0-87169-209-0 (page 123)
^ Weisstein, Eric W. "Icosahedral group". MathWorld.
^ Weisstein, Eric W. "Zome". MathWorld.
^ Read, R. C.; Wilson, R. J. (1998), An Atlas of Graphs, Oxford University Press, p. 269
References
Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (Section 3-9)
Cromwell, P. (1997). Polyhedra. United Kingdom: Cambridge. pp. 79–86 Archimedean solids. ISBN 0-521-55432-2.
The Big Bang Theory Series 8 Episode 2 - The Junior Professor Solution: features this solid as the answer to an impromptu science quiz the main four characters have in Leonard and Sheldon's apartment, and is also illustrated in Chuck Lorre's Vanity Card #461 at the end of that episode.
External links
Eric W. Weisstein, Small Rhombicosidodecahedron (Archimedean solid) at MathWorld.
- Weisstein, Eric W. "Small rhombicosidodecahedron graph". MathWorld.
Klitzing, Richard. "3D convex uniform polyhedra x3o5x - srid".
- Editable printable net of a Rhombicosidodecahedron with interactive 3D view
- The Uniform Polyhedra
Virtual Reality Polyhedra The Encyclopedia of Polyhedra- The Rhombi-Cosi-Dodecahedron Website
- The Rhombicosidodecahedron as a 3D puzzle



















